LamaConv—Logics and Automata Converter Library
LamaConv (internal code name RltlConv) is a Java library that is capable of translating expressions in temporal logics into equivalent automata and to generate monitors out of these automata. These monitors can be used for runtime verification and model checking.
Supported automata and logics as well as possible conversions
The green boxes are logics which are currently supported. These are Regular Expressions (RegEx), Omega Regular Expressions (omega-RegEx), the Linear Temporal Logic (LTL), the Linear Temporal Logic with past (pLTL), the Regular Linear Temporal Logic (RLTL) and the Regular Linear Temporal Logic wth past (pRLTL).
The blue boxes are automata where the right A's stand for automata, the D for deterministic, the N for non-deterministic, the left A's for alternating, the F for finite, the B for Büchi, the P for parity, the S for Streett, the R for Rabin and the 2 for two-way. The 3 in A3PA means that the automaton only has at most three different parities, 3 and 4 in Moore and Mealy means that the automaton has 3 or 4 different output values and the epsilon means that epsilon transitions can exist in those automata.
The edges stand for the following: Black edges mean that this transition is available, red edges are describing transformations that are under construction or at least planned and loops show that an automaton can be minimized into at least a local minimum. The double transition from DFA to 3DMoore shows that two DFAs are needed to create a Moore machine. This is the monitor construction for the three-valued semantics of LTL, LTL3. The stars between RLTL and epsilon-ABA and pRLTL and epsilon-2-ABA mean that a Büchi automaton instead of a parity automaton with three parities can be directly created if only finite delay languages are used in the RLTL formula. The way from A3PA to ASA, marked by a §, is only used if the A3PA has the parities 0, 1 and 2 and the way from the A3PA to the ARA, marked by a ¶, is used if the A3PA has the parities 1, 2 and 3.
Tutorial / Appetizer
RltlConv is deployed as a single jar containing all its dependencies. You can start RltlConv either by manually typing java -jar rltlconv.jar or using the shell/batch script as follows:
> ./rltlconv.sh
Calling the application without any argument will result in a description of the command line interface.
Usage: rltlconv [@filename|input] operators ... If an input (not starting with an @ sign) is given the input is used directly as input string. If a filename (starting with an @ sign) is given the input is read from the file specified. If neither a direct input nor a filename is given, the input is read from stdin. Operators are applied on the input in the given order, the result is printed to stdout. Available operators are: ...
In this tutorial we will use the LTL formula pUq with the informal semantics of the atomic proposition p holding until the atomic proposition q holds. As a first operation we can input this formula to RltlConv and use the operation --formula on it.
> ./rltlconv.sh "LTL=pUq" --formula
As the input already is a formula, this has no other effect then pretty printing the input.
LTL = p U q, ALPHABET = [p, q]
The alphabet was guessed from the used atomic propositions in the formula. If we want to specify the alphabet explicitly we can do this as follows:
> ./rltlconv.sh "LTL=pUq,ALPHABET=[p,q,r]" --formula
The output still contains only a pretty print:
LTL = p U q, ALPHABET = [p, q, r]
The given alphabet must at least contain all atomic propositions used in the formula:
> ./rltlconv.sh "LTL=pUq,ALPHABET=[p]" --formula
This input creates the error
Sign q could not be found in alphabet.
In all the above cases the alphabet is the set of atomic propositions available. If we consider input words based on this alphabet one letter of this word is exactly one atomic proposition of the alphabet. Such a word has the informal semantics of events, because there cannot be two events at the same time. If we want to use the atomic propositions with the informal semantics of variables which can be assigned values in each step of the execution, the input word would be a sequence of sets containing the variables which are evaluated to true in the current step. In other words the alphabet would be the power set of the given set of available atomic propositions. We can handle the latter case in RltlConv using the operation --props
> ./rltlconv.sh "LTL=pUq" --props
As a result we still get only a pretty print of the formula, but the alphabet annotation contains the power set of the atomic propositions used in the formula.
LTL = p U q, ALPHABET = [(), (p), (q), (p&&q)]
(Note: We use the events semantic for the rest of this tutorial.)
Next step is translating the LTL formula into an equivalent alternating Büchi automaton (ABA).
> ./rltlconv.sh "LTL=pUq" --formula --apa
Actually the operation --apa does not generate alternating Büchi automata, but alternating parity automata with the parities 1 and 2. The parity 1 can be understood as non accepting state and the parity 2 as accepting state, as long as no other parities are involved.
APA {
ALPHABET = ["p", "q"]
STATES = [q0:1]
START = q0
DELTA(q0, "p") = FALSE OR (TRUE AND q0)
DELTA(q0, "q") = TRUE OR (FALSE AND q0)
}
The output will be printed using the Automata File Format (AFF) as described in ???.
Such an ABA can now be translated into an equivalent Büchi automaton (NBA) using the operation --nba.
> ./rltlconv.sh "LTL=pUq" --formula --apa --nba
The result is as expected:
NBA {
ALPHABET = ["p", "q"]
STATES = [q0x, x: ACCEPTING]
START = [q0x]
DELTA(q0x, "p") = [q0x]
DELTA(q0x, "q") = [x]
DELTA(x, "p") = [x]
DELTA(x, "q") = [x]
}
NBAs can be minimized using the operation --min
> ./rltlconv.sh "LTL=pUq" --formula --apa --nba --min
As a result we get the a much smaller NBA:
NBA {
ALPHABET = ["p", "q"]
STATES = [q0: ACCEPTING, q1]
START = [q1]
DELTA(q0, "p") = [q0]
DELTA(q0, "q") = [q0]
DELTA(q1, "p") = [q1]
DELTA(q1, "q") = [q0]
}
Obvious steps in the translation can be left out in the chain of operations. For example if you want to translate an LTL formula into an equivalent NBA this is only possible (in RltlConv) by translating the LTL formula into an ABA first.
> ./rltlconv.sh "LTL=pUq" --formula --nba --min
Leads to the same result as the above statement.
To get a better idea of the output automata we can translate them into the GraphViz input format.
> ./rltlconv.sh "LTL=pUq" --formula --nba --min --dot
The output looks as follows.
digraph G {
rankdir=LR;
q0 [shape=doublecircle, margin=0];
q1 [shape=circle, margin=0];
start0 [shape=none, style=invis];
start0 -> q1 [label="START"];
q0 -> q0 [label="\"p\""];
q0 -> q0 [label="\"q\""];
q1 -> q1 [label="\"p\""];
q1 -> q0 [label="\"q\""];
}
This can be used as input in the tool dot of GraphViz.
Luckily we do not need to call dot on out own, but can just use the operation --pdf instead of --dot.
> ./rltlconv.sh "LTL=pUq" --formula --nba --min --pdf
As the result is the content of a PDF file it is strongly recommended to pipe it into a file.
> ./rltlconv.sh "LTL=pUq" --formula --nba --min --pdf > foo.pdf
Other possible options are --svg and --png.
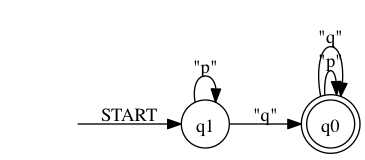
In the next step we will perform an emptiness per state test on the Büchi automaton. The emptiness per state test on Büchi automata is an important part of the LTL3 automata construction as described in the LTL3 paper ???. As a result we will get an nondeterministic finite automaton (NFA) with the same structure as the minimized NBA, but with every non-empty-state marked as as accepting. During the emptiness per state test a state is considered empty is the Büchi automaton does accept the empty language if you start its execution in this particular state.
> ./rltlconv.sh "LTL=pUq" --formula --nba --min --nfa --pdf > foo.pdf
As expected in the result both states are accepting.
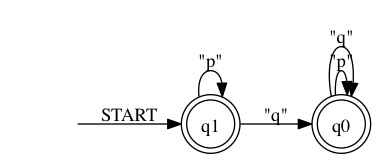
This NFA can now be translated into an equivalent deterministic finite automaton (DFA).
> ./rltlconv.sh "LTL=pUq" --formula --nba --min --nfa --dfa --pdf > foo.pdf
The result looks exactly the same as in this particular example the NFA is already deterministic.
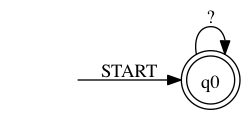
This DFA can now be minimized. The result will be the unique minimized automaton accepting the same language as the given one.
> ./rltlconv.sh "LTL=pUq" --formula --nba --min --nfa --dfa --min
In this case the automaton accepts everything. (Note that the emptiness per state test differs from the other translation. Most operations return language equivalent automata, the emptiness per state test does not!)
Performing the LTL3 automata construction we need the DFA generated from the emptiness per state test on the NBA, which is language equivalent with the given LTL formula, and the DFA generated the same way from the negated LTL formula. This can be achieved by using the --nbas operation which creates both NBAs.
> ./rltlconv.sh "LTL=pUq" --formula --nbas --pdf > foo.pdf
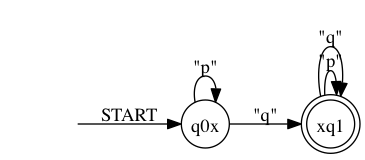
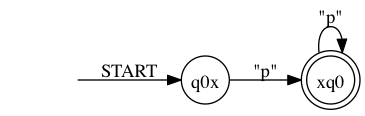
To check this result you can compare the second automaton with the output of the following statement, where the LTL formula is negated manually.
> ./rltlconv.sh "LTL=!(pUq)" --formula --nba --pdf > foo.pdf
As next steps we perform the same operations as before starting with minimizing the NBAs.
> ./rltlconv.sh "LTL=pUq" --formula --nbas --min --pdf > foo.pdf
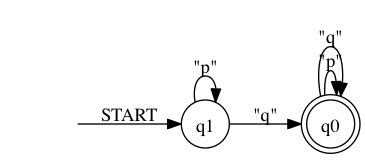
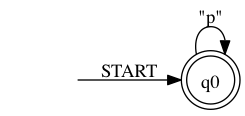
Now we perform the emptiness per state test on both NBAs.
> ./rltlconv.sh "LTL=pUq" --formula --nbas --min --nfas --pdf > foo.pdf
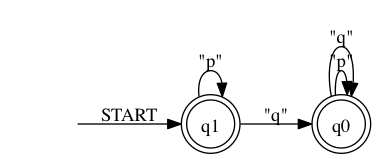
Next step is determinizing and minimizing them.
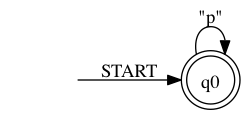
> ./rltlconv.sh "LTL=pUq" --formula --nbas --min --nfas --dfas --min --pdf > foo.pdf
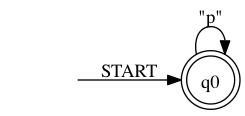
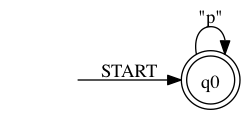
Now we can use both DFAs to generate one moore monitor out of them.
> ./rltlconv.sh "LTL=pUq" --formula --nbas --min --nfas --dfas --min --moore --pdf > foo.pdf
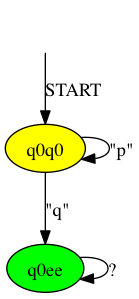
The result can be minimized using the --min operator. Minimizing moore machines creates unique minimized machines.
> ./rltlconv.sh "LTL=pUq" --formula --nbas --min --nfas --dfas --min --moore --min --pdf > foo.pdf
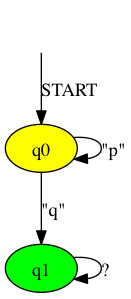
As mentioned before the obvious parts in the translation can be left out.
> ./rltlconv.sh "LTL=pUq" --formula --moore --min --pdf > foo.pdf
Creates the same result as before.
To create a more interesting monitore we add one more sign to the alphabet.
> ./rltlconv.sh "LTL=pUq,ALPHABET=[p,q,r]" --formula --moore --min --pdf > foo.pdf
Coming to something completely different we now use this formula and translate it into an alternating mealy machine using the FLTL4 semantics as defined in ???
> ./rltlconv.sh "LTL=pUq,ALPHABET=[p,q,r]" --formula --amealy --pdf > foo.pdf
Allternating mealy machines can be translated into deterministic mealy machines using the --mealy operation.
> ./rltlconv.sh "LTL=pUq,ALPHABET=[p,q,r]" --formula --amealy --mealy --pdf > foo.pdf
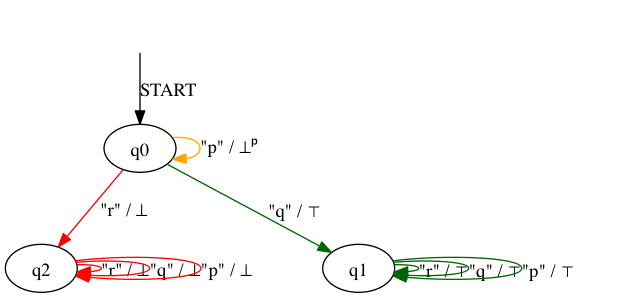
Deterministic mealy machines can be minimized using the --min option. The result will be the unique minimized mealy machine.
> ./rltlconv.sh "LTL=pUq,ALPHABET=[p,q,r]" --formula --amealy --mealy --min --pdf > foo.pdf
Same result as above as the resulting mealy machine in this particular example is already minimized.
As always you can omit the obvious parts.
> ./rltlconv.sh "LTL=pUq,ALPHABET=[p,q,r]" --formula --mealy --pdf > foo.pdf
Same result as above.
Authors
LamaConv is developed at the ISP under the lead of Torben Scheffel and Malte Schmitz with contributions from Sebastian Hungerecker and the students Chistopher Krüger, Johannes Thorn, Marco Kabelitz, Jan Gröschner and Alfredo Maceratesi (in arbitrary order).
Download
The archive contains one jar archive containing the compiled source with all dependencies. The dependencies in detail are: Scala Standard Library, SALT and Reduce. You need at least Java 1.7 to run the code.
Installation
- Install graphviz and make sure that
dotis available in your path. - Download the archive above and use the contained
jarfile either direct or through the provided start scripts.
Web Application
The web application on vm05.isp.uni-luebeck.de uses SALT and LamaConv to build LTL3 and FLTL4 monitors.
Publications and Further Information
- A publication on a distributed runtime verification approach using LamaConv can be found at the LEGO® meets RV project page.
- Logics for distributed Runtime-Verification (Master thesis of Torben Scheffel on the theoretical background of LEGO® meets RV, German language)
- Distributed Runtime Verification on Embedded Systems (Master thesis of Malte Schmitz on LEGO® meets RV, German language)
- Specification of the Automata File Format (AFF) in EBNF
- Transformation of Regular Linear Temporal Logic into Parity Automata (Bachelor thesis of Malte Schmitz, German language)
- Transformation of Parity Automata into Büchi-Automata (Bachelor thesis of Torben Scheffel, German language)
- Runtime-Verification with a four-valued semantics for the Regular Linear Temporal Logic (Master thesis of Christopher Krüger, German language)
- From 2-Way Nondeterministic Büchi Automata to Alternating Büchi Automata (Bachelor thesis of Marco Kabelitz)
Contact
If you have further questions, problems using the software provided on this page or want to extend it in some way, feel free to contact Torben Scheffel or Malte Schmitz.